![[자료구조] AVL 트리](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FkOmhu%2FbtrSM4ap7Ed%2FmBq2BWKM6DkYmPXHGJrKpK%2Fimg.jpg)

AVL 트리란?
AVL 트리는 트리가 비균형 상태로 되면 스스로 노드들을 재배치해 균형 상태로 만듭니다.
이 탐색 기법에서는 균형 인수라는 것을 정의합니다.
균형 인수 (Balance Factor) = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
모든 노드의 균형 인수가 $\pm 1$ 이하이면 AVL 트리입니다.
여담으로, Adelson-Velskii와 Landis의 제안자 이름을 따 AVL이라고 지어졌습니다.
AVL 트리 구현
AVL 트리의 핵심은 균형 인수를 1 이하로 맞추는 것입니다.
AVL 트리인 상태에서 균형 인수가 깨지게 될 경우는 삽입 연산, 삭제 연산 총 두 가지입니다. 연산을 수행하고 생기는 결과의 경우에 따라 균형 인수를 1 이하로 맞출 수 있도록 대응해주면 됩니다.
그렇다면 어떻게 균형 인수를 다시 1 이하로 맞춰줄 수 있을까요?
연산이 이루어진 노드의 조상 노드 중 균형 인수가 2 이상이 된 가장 가까운 조상 노드의 서브 트리들을 회전 시키면 됩니다.
서브 트리 회전

서브 트리는 아래와 같이 왼쪽, 오른쪽으로 회전시킬 수 있습니다.


구현한 코드는 다음과 같습니다.
AVLNode *rotate_left(AVLNode *parent) {
AVLNode *child = parent->right;
parent->right = child->left;
child->left = parent;
return child;
}
AVLNode *rotate_right(AVLNode *parent) {
AVLNode *child = parent->left;
parent->left = child->right;
child->right = parent;
return child;
}
서브 트리를 회전하는 함수를 통해 AVL 트리에서 균형 인수를 맞추기 위해 다음의 4가지 경우에 대응할 수 있습니다.
- LL 타입
- RR 타입
- LR 타입
- RL 타입
하나씩 알아보도록 하겠습니다. 편의를 위해 설명 중 R은 서브 트리의 루트 노드, N은 새롭게 추가되는 노드라고 간주하겠습니다.
LL 타입
LL 타입은 R - 왼쪽 자식 - 왼쪽 자식자리에 노드가 추가되면서 발생합니다.

균형 인수를 맞추려면 해당 서브 트리를 오른쪽으로 회전하면 됩니다.
if(balance > 1 && key < node->left->key) {
return rotate_right(node);
}
RR 타입
RR 타입은 R - 오른쪽 자식 - 오른쪽 자식자리에 노드가 추가되면서 발생합니다.

균형 인수를 맞추려면 해당 서브 트리를 왼쪽으로 회전하면 됩니다.
if(balance < -1 && key > node->right->key) {
return rotate_left(node);
}
LR 타입
LR 타입은 R - 왼쪽 자식 - 오른쪽 자식자리에 노드가 추가되면서 발생합니다.

이 상태에서 노드 A를 기준으로 왼쪽으로 회전시키면 LL 타입이 나오게 됩니다. 그 때 R에서 오른쪽으로 회전시키면 됩니다.
if(balance > 1 && key > node->left->key) {
node->left = rotate_left(node->left);
return rotate_right(node);
}
RL 타입
RL 타입은 R - 오른쪽 자식 - 왼쪽 자식자리에 노드가 추가되면서 발생합니다.
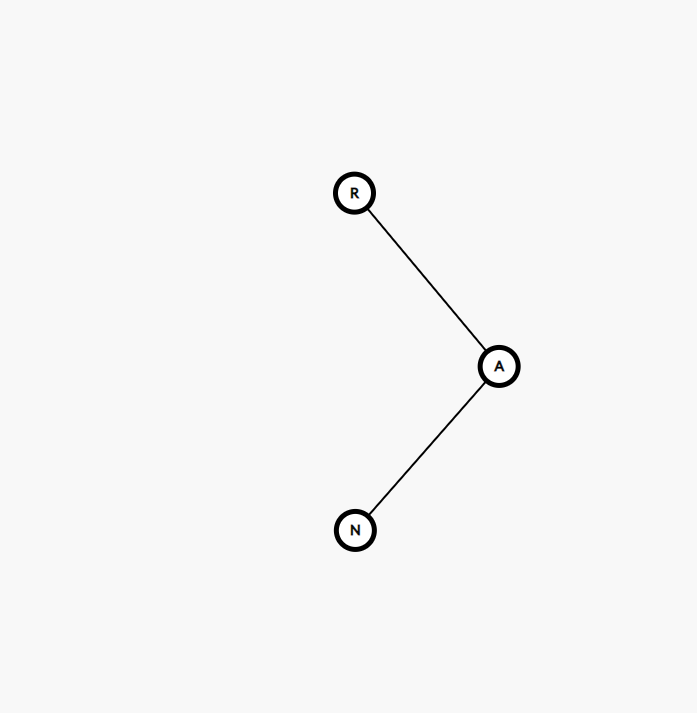
이 상태에서 노드 A를 기준으로 오른쪽으로 회전시키면 RR 타입이 나오게 됩니다. 그 때 R에서 왼쪽으로 회전시키면 됩니다.
if(balance < -1 &&. key < node->right->key) {
node->right = rotate_right(node->right);
return rotate_left(node);
}
AVL 트리의 시간복잡도
AVL 트리는 균형 트리가 항상 보장되기 때문에 탐색이 $O(log \space n)$시간 안에 끝나게 됩니다.
'CSE > 자료구조 (data structure)' 카테고리의 다른 글
| [자료구조] 해시 함수 (hash function) (0) | 2022.11.26 |
|---|---|
| [자료구조] 해싱 (hashing) (0) | 2022.11.25 |
| [자료구조] 보간 탐색 (interpolation search) (0) | 2022.11.21 |
| [자료구조] 색인 순차 탐색 (indexed sequential search) (0) | 2022.11.20 |
| [자료구조] 이진 탐색 (binary search) (0) | 2022.11.19 |

컴퓨터 전공 관련, 프론트엔드 개발 지식들을 공유합니다. React, Javascript를 다룰 줄 알며 요즘에는 Typescript에도 관심이 생겨 공부하고 있습니다. 서로 소통하면서 프로젝트 하는 것을 즐기며 많은 대외활동으로 개발 능력과 소프트 스킬을 다듬어나가고 있습니다.
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 해시 함수 (hash function)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FGfgx6%2FbtrSJyQ8UDk%2FlLxrIZsVVGoUGQKgTX1VnK%2Fimg.jpg)
![[자료구조] 해싱 (hashing)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FX24Lf%2FbtrSHYpH03z%2FeaEsbHCaadc3bHun1fK9V1%2Fimg.jpg)
![[자료구조] 보간 탐색 (interpolation search)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbsxXOu%2FbtrSJn3l0sg%2FHK3xNgg0OCG7srz4CoGy4k%2Fimg.jpg)
![[자료구조] 색인 순차 탐색 (indexed sequential search)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4lef5%2FbtrSJTnfQxJ%2F5XSfZXq8YHI3VKEcyK9R7k%2Fimg.jpg)