![[자료구조] 최소 신장 트리 (MST; Minimum Spanning Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FLmONF%2FbtrQfJUz2SY%2FZDilij7gm2qJ1S2zz5FbOk%2Fimg.png)


신장 트리 (Spanning Tree)
신장 트리는 그래프 내의 모든 정점을 포함하는 트리입니다. 다만 아래의 조건들을 만족해야 합니다.
- 모든 정점들이 연결되어 있어야 함
- 사이클을 포함하면 안 됨
- n개의 정점을 n-1개의 간선으로 연결해야 함
해당 조건만 만족하면 되므로 하나의 그래프에는 다양한 신장 트리가 존재할 수 있습니다.

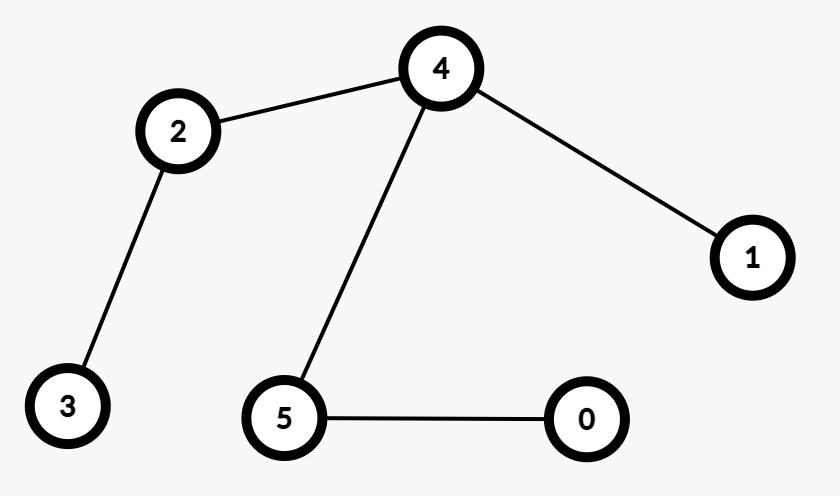


최소 신장 트리 (MST; Minimum Spanning Tree)
최소 신장 트리는 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결한 트리입니다. 최소 신장 트리를 구하는 방법으로는 Kruskal과 Prim이 고안한 알고리즘이 대표적으로 사용되고 있습니다.
Union-Find
최소 신장 트리를 구하기 위해서 union-find라는 연산을 해야 합니다.
union-find 연산은 union 연산과 find 연산으로 나눌 수 있습니다.
- union(x, y): 원소 x와 y가 속해있는 집합을 입력으로 받아 2개의 집합의 합집합을 만듬.
- find(x): 원소 x가 속해있는 집합을 반환함.
찾으려는 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지 안 하는지 체크해야 합니다.
간선이 서로 다른 집합에 속하는 정점을 연결하면 사이클이 형성되지 않습니다. 그래서 추가하려는 간선의 양끝 정점이 같은 집합에 속해있는지 검사해야 합니다.
int parent[MAX_VERTICES] // 부모 노드
void set_init(int n) {
for (int i = 0; i < n; i++) {
parent[i] = -1;
}
}
// curr가 속한 집합 반환
int set_find(int curr) {
if(parent[curr] == -1) {
return curr;
}
while(parent[curr] != -1) curr = parent[curr];
return curr;
}
// 두 개의 원소가 속한 집합을 합침
void set_union(int a, int b) {
int root1 = set_find(a); // 노드 a의 루트를 찾는다.
int root2 = set_find(b); // 노드 b의 루트를 찾는다.
if(root1 != root2) { // 합한다.
parent[root1] = root2;
}
}
시간 복잡도 분석
Kruskal과 Prim 알고리즘의 시간 복잡도를 알아보겠습니다.
Kruskal은 연결되어 있는 간선들의 가중치를 오름차순으로 정렬해야 하므로 퀵 정렬의 소요 시간인 $e \times log_{2} e$ 만큼의 시간이 소요 됩니다. 따라서 $O(e log_{2} e)$의 시간 복잡도를 가집니다.
Prim은 위의 코드에서는 이중 반복문에 의해 $O(n^2)$의 시간 복잡도를 가집니다. 하지만 distance 배열을 우선순위 큐로 변경한다면 최소 힙을 구성하는 시간인 $O(E log V)$의 시간 복잡도를 가집니다.
'CSE > 자료구조 (data structure)' 카테고리의 다른 글
| [자료구조] 프림(Prim)의 MST 알고리즘 (0) | 2022.11.05 |
|---|---|
| [자료구조] 크루스칼(Kruskal)의 MST 알고리즘 (0) | 2022.11.04 |
| [자료구조] 허프만 코드 (Huffman Code) (0) | 2022.10.20 |
| [자료구조] 힙 (Heap) (0) | 2022.10.20 |
| [자료구조] 이진 탐색 트리 (BST; Binary Search Tree) (0) | 2022.10.19 |

컴퓨터 전공 관련, 프론트엔드 개발 지식들을 공유합니다. React, Javascript를 다룰 줄 알며 요즘에는 Typescript에도 관심이 생겨 공부하고 있습니다. 서로 소통하면서 프로젝트 하는 것을 즐기며 많은 대외활동으로 개발 능력과 소프트 스킬을 다듬어나가고 있습니다.
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 프림(Prim)의 MST 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbFG405%2FbtrQcM6jTT3%2FK6HAyIEKvCUDQQQ6ig82Lk%2Fimg.png)
![[자료구조] 크루스칼(Kruskal)의 MST 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FU0Xj4%2FbtrQeChAyHp%2FGGKij1x57h1a3ZQIqBb5T0%2Fimg.png)
![[자료구조] 허프만 코드 (Huffman Code)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FtiHlE%2FbtrPfYmkhXw%2FbWGJY7P29CDRKCsKK2MAr1%2Fimg.png)
![[자료구조] 힙 (Heap)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FTCT5Q%2FbtrPtJ2a4G4%2FH0KT7mrj7fs9LTn5RTmKIk%2Fimg.png)