![[자료구조] 이진 트리 (Binary Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fcd3Phq%2FbtrPgWuuAwk%2F5ZkAFiyw2DSgSF2fPkfzkK%2Fimg.png)


이진 트리의 정의
모든 노드가 2개의 서브 트리를 가지고 있는 트리입니다.
서브 트리는 공집합일 수 있습니다. 따라서 이진 트리의 노드에는 최대 2개까지의 자식 노드가 존재할 수 있고 모든 노드의 차수가 2 이하가 됩니다. 따라서 트리의 차수도 2 이하가 됩니다. 공집합도 이진 트리라는 점에 주의합시다.
또한, 이진 트리에는 서브 트리간의 순서가 존재합니다. 따라서 왼쪽 서브 트리와 오른쪽 서브 트리는 서로 구별됩니다.
이진 트리의 정의
1. 공집합이거나,
2. 루트와 왼쪽 서브 트리, 오른쪽 서브 트리로 구성된 노드들의 유한 집합으로 정의된다. 이진 트리의 서브 트리들은 모두 이진 트리여야 한다.
이진 트리의 성질
- $n$개의 노드를 가진 이진 트리는 $n-1$개의 간선을 가집니다.
- 높이가 $h$인 이진 트리의 경우, 최소 h개의 노드를 가지며 최대 $2^h-1$개의 노드를 가집니다.
2번 내용 증명
한 레벨에는 적어도 하나의 노드가 존재해야 하므로 높이가 $h$인 이진 트리는 적어도 $h$개의 노드를 가진다. 또한, 하나의 노드는 최대 2개의 자식을 가질 수 있으므로 레벨 $i$에서의 노드의 최대 개수는 $2^{i-1}$이 된다.
→ 전체 노드 개수: $\Sigma_{i=1}^{k}2^{i-1}=2^k-1$
이진 트리의 분류
- 포화 이진 트리(Full binary tree)
- 완전 이진 트리(Complete binary tree)
- 기타 등등..
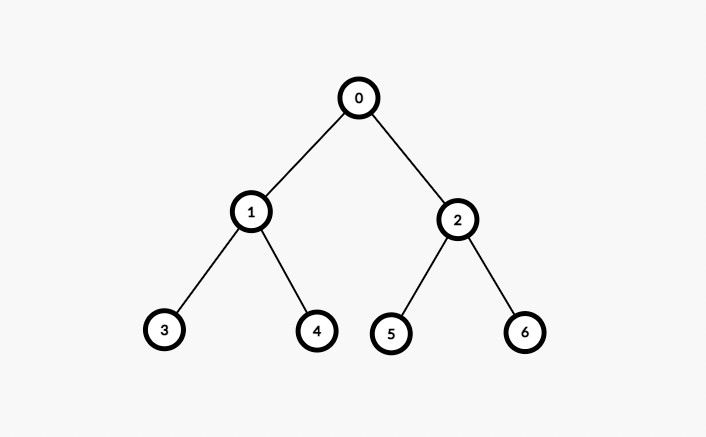
포화 이진 트리
포화 이진 트리는 용어 그대로 트리의 각 레벨에 노드가 꽉 차있는 이진 트리를 의미합니다. 즉, 높이 $k$인 포화 이진 트리는 정확하게 $2^k-1$개의 노드를 가집니다 .

포화 이진 트리에는 다음과 같이 각 노드에 번호를 붙일 수 있습니다. 노드에 번호를 부여하는 방법은 레벨 단위로 왼쪽에서 오른쪽으로 번호를 붙이면 됩니다. 그리고 이 번호는 항상 일정합니다.
ex) 루트 노드의 오른쪽 자식 노드의 번호는 항상 2이다.
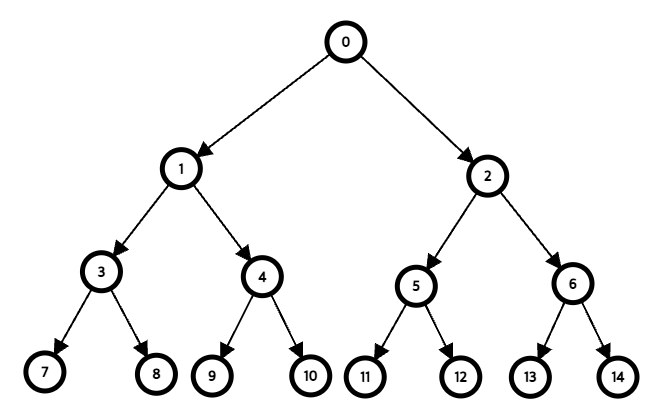
완전 이진 트리
완전 이진 트리는 높이가 $k$일 때 레벨 1부터 $k-1$까지는 노드가 모두 채워져 있고 마지막 레벨 $k$에서 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진 트리입니다. 마지막 레벨에서는 노드가 꽉 차있지 않아도 되지만 중간에 빈곳이 있으면 안됩니다. 따라서 포화 이진 트리는 항상 완전 이진트리이지만 그 역은 항상 성립하지 않습니다.
이진 트리의 표현
이진 트리를 프로그램으로 어떻게 표현하는지 알아봅시다.
- 배열을 이용하는 방법
- 포인터를 이용하는 방법
배열 표현법
저장하고자 하는 이진 트리를 완전 이진 트리라고 가정하고 이진 트리의 깊이가 k이면 $2^{k-1}$개의 공간을 연속적으로 할당한 다음, 완전 이진 트리의 번호대로 저장합니다.
부모와 자식의 index 관계를 알면 탐색하는데 도움이 됩니다.
부모와 자식 사이 index 관계로 알아보기
노드 $i$의 부모 노드 인덱스 → $i/2$
노드 $i$의 왼쪽 자식 노드 인덱스 → $2i$
노드 $i$의 오른쪽 자식 노드 인덱스 → $2i+1$
링크 표현법
트리에서의 노드가 구조체로 표현되고, 각 노드가 포인터를 가지고 있어서 이를 이용하여 노드와 노드를 연결하는 방법입니다.
이진 트리를 링크 표현법으로 표현하면 다음과 같이 하나의 노드가 3개의 필드를 가집니다(데이터를 저장하는 필드, 왼쪽 자식 노드와 오른쪽 자식 노드를 가리키는 각각의 포인터 필드).

이진 트리를 링크 표현법으로 다시 그려보면 다음과 같습니다.

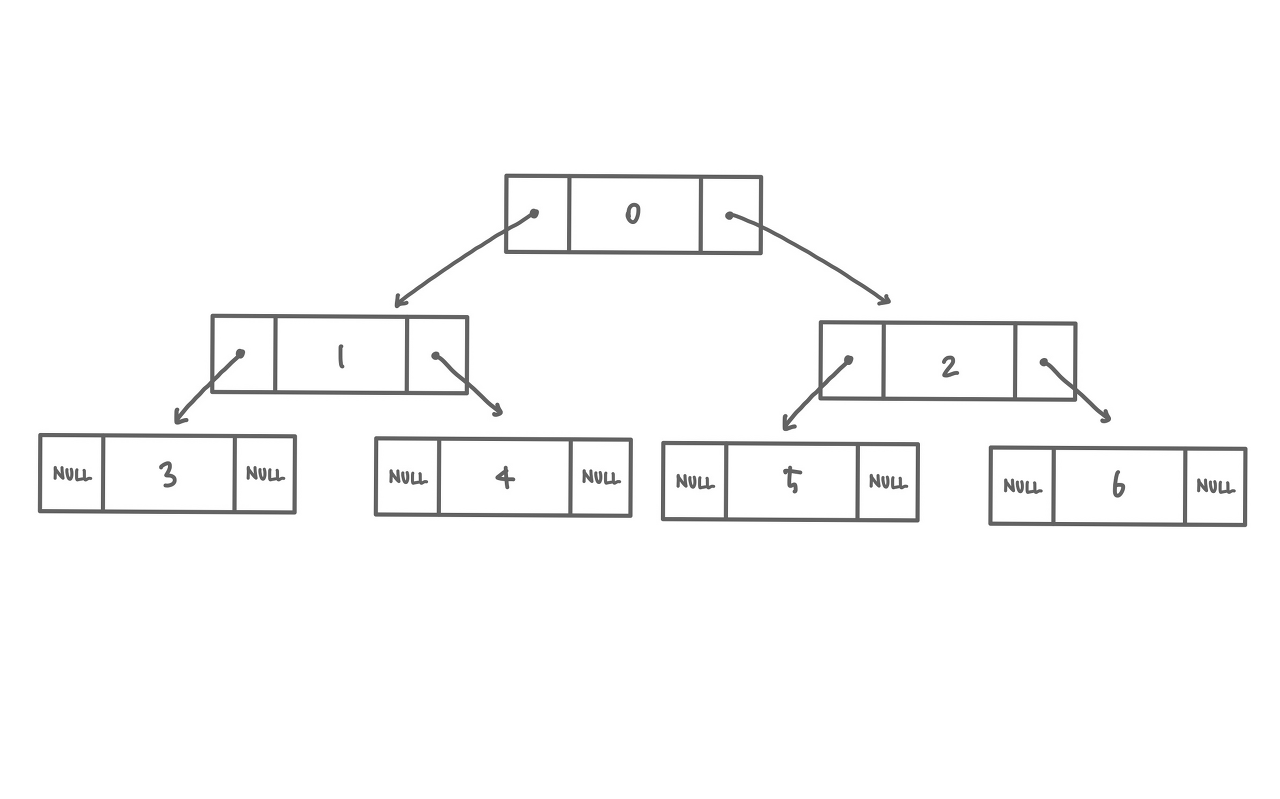
이를 C언어로 나타내기 위해 구조체와 포인터 개념을 이용해야 합니다.
구조체를 이용하여 노드의 구조를 정의하고, 포인터의 개념을 이용하여 링크를 정의하면 됩니다.
typedef struct TreeNode {
int data;
struct TreeNode *left, *right;
} TreeNode;
링크법으로 표현된 트리는 루트 노드를 가리키는 포인터만 있으면 모든 노드들에 접근할 수 있습니다.
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct TreeNode {
int data;
struct TreeNode *left, *right;
} TreeNode;
int main() {
TreeNode *n1, *n2, *n3;
n1->data = 10;
n1->left = n2;
n1->right = n3;
n2->data = 20;
n2->left = null;
n2->right = null;
n3->data = 30;
n3->left = null;
n3->right = null;
}'CSE > 자료구조 (data structure)' 카테고리의 다른 글
| [자료구조] 이진 탐색 트리 (BST; Binary Search Tree) (0) | 2022.10.19 |
|---|---|
| [자료구조] 이진 트리 순회 (0) | 2022.10.18 |
| [자료구조] 트리 (Tree) (2) | 2022.10.16 |
| [자료구조] 이중 연결 리스트 (Double Linked List) (0) | 2022.10.09 |
| [자료구조] 원형 연결 리스트 (Circular Linked List) (0) | 2022.10.08 |

컴퓨터 전공 관련, 프론트엔드 개발 지식들을 공유합니다. React, Javascript를 다룰 줄 알며 요즘에는 Typescript에도 관심이 생겨 공부하고 있습니다. 서로 소통하면서 프로젝트 하는 것을 즐기며 많은 대외활동으로 개발 능력과 소프트 스킬을 다듬어나가고 있습니다.
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 이진 탐색 트리 (BST; Binary Search Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FC681y%2FbtrPhpDiT3B%2FW9e7Pt0gkQZKNkjpofhZk1%2Fimg.png)
![[자료구조] 이진 트리 순회](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdSr2dw%2FbtrPgZ5Zghu%2F9Pv7xXjHurHUGAGPCKsJG0%2Fimg.png)
![[자료구조] 트리 (Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcoKGVp%2FbtrPhoLcOvB%2FlUdFvvK7PyYEm9fFUHKb8k%2Fimg.png)
![[자료구조] 이중 연결 리스트 (Double Linked List)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FPUjaF%2FbtrPf41eNb8%2F6ro28iOLdt6xK70bVPO63K%2Fimg.png)