![[자료구조] 다익스트라(Dijkstra)의 최단 경로 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FyogTF%2FbtrQd82UTIH%2FV1EgjO7MKAF9zioVjJrgUk%2Fimg.png)


최단 경로
네트워크 상에서 정점 v와 정점 w를 연결하는 경로 중 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제입니다.
최단 경로를 찾는 방법 중 Dijkstra, Floyd-Warshall가 고안한 알고리즘이 대표적으로 사용되고 있습니다.
Dijkstra의 최단 경로 알고리즘
최단 경로를 찾는 과정은 다음과 같습니다.
- 출발 노드를 설정
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장
- 방문하지 않은 노드 중, 특정 노드로 가는 가장 비용이 적은 간선 선택
- 새로 발견한 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 가중치로 갱신
- 모든 노드를 방문할 때까지 3번과 4번 반복
예시로 한 그래프를 Dijkstra의 알고리즘을 이용해 최단 경로를 구해보겠습니다.
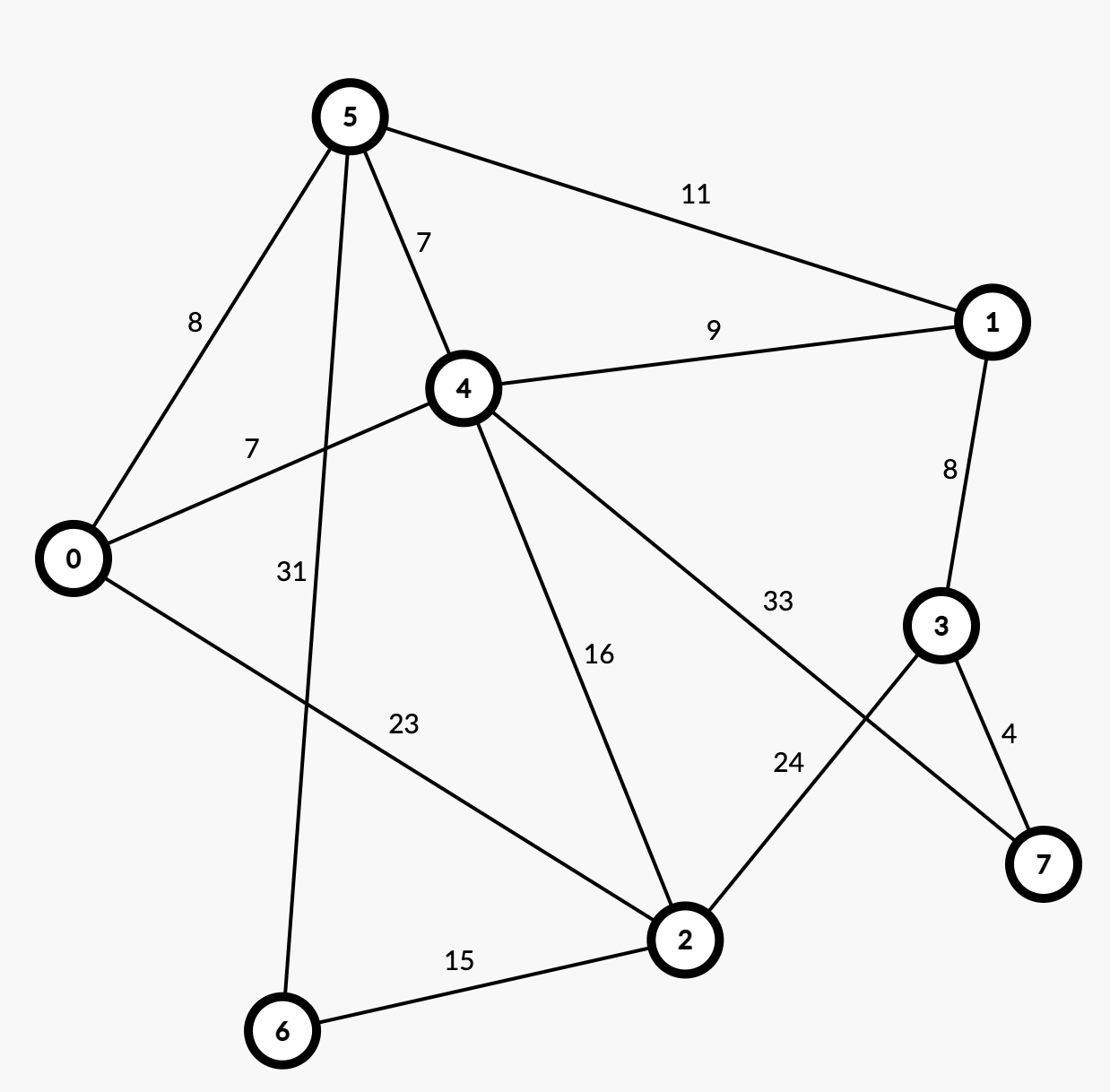
Dijkstra 알고리즘은 시작 정점에서 다른 정점으로 가는 최단거리를 기록하는 배열이 필요합니다.

각 정점에서 다른 정점으로 이동할 때 걸리는 가중치를 표로 표현한 것입니다.

표 위의 그래프와 비교해봅시다. 예를 들어, 0번 정점과 2번 정점의 간선 가중치를 확인해보면 23인 것을 알 수 있습니다. 또한 무방향 그래프를 표에 옮겼으므로 위 아래가 대칭임을 파악할 수 있습니다.
Dijkstra 알고리즘으로 최단 경로를 구하려면 시작 정점을 정해야 합니다. 정점 0에서 시작해보도록 하겠습니다. (이해를 돕기 위해 발견된 정점은 하늘색으로 색칠이 되어있고, 갱신된 간선의 가중치는 빨간색 글씨로 표시했습니다.)


정점 $\{0\}$에서 가장 가중치가 낮은 간선은 정점 4로 가는 간선입니다. 그렇다면 이제 정점 4를 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신한 결과 두 노드로 가는 총 가중치가 바뀐 것을 알 수 있습니다(시작 정점 -> 정점 1, 시작 정점 -> 정점 7)


정점 $\{0, 4\}$에서 가장 가중치가 낮은 간선은 정점 5로 가는 간선입니다. 그렇다면 이제 정점 5를 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신한 결과 한 노드로 가는 총 가중치가 바뀐 것을 알 수 있습니다(시작 정점 -> 정점 5 -> 정점 6)


정점 $\{0, 4, 5\}$에서 가장 가중치가 낮은 간선은 정점 1로 가는 간선입니다. 그렇다면 이제 정점 1을 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신한 결과 한 노드로 가는 총 가중치가 바뀐 것을 알 수 있습니다(시작 정점 -> 정점 4 -> 정점 1 -> 정점 3)

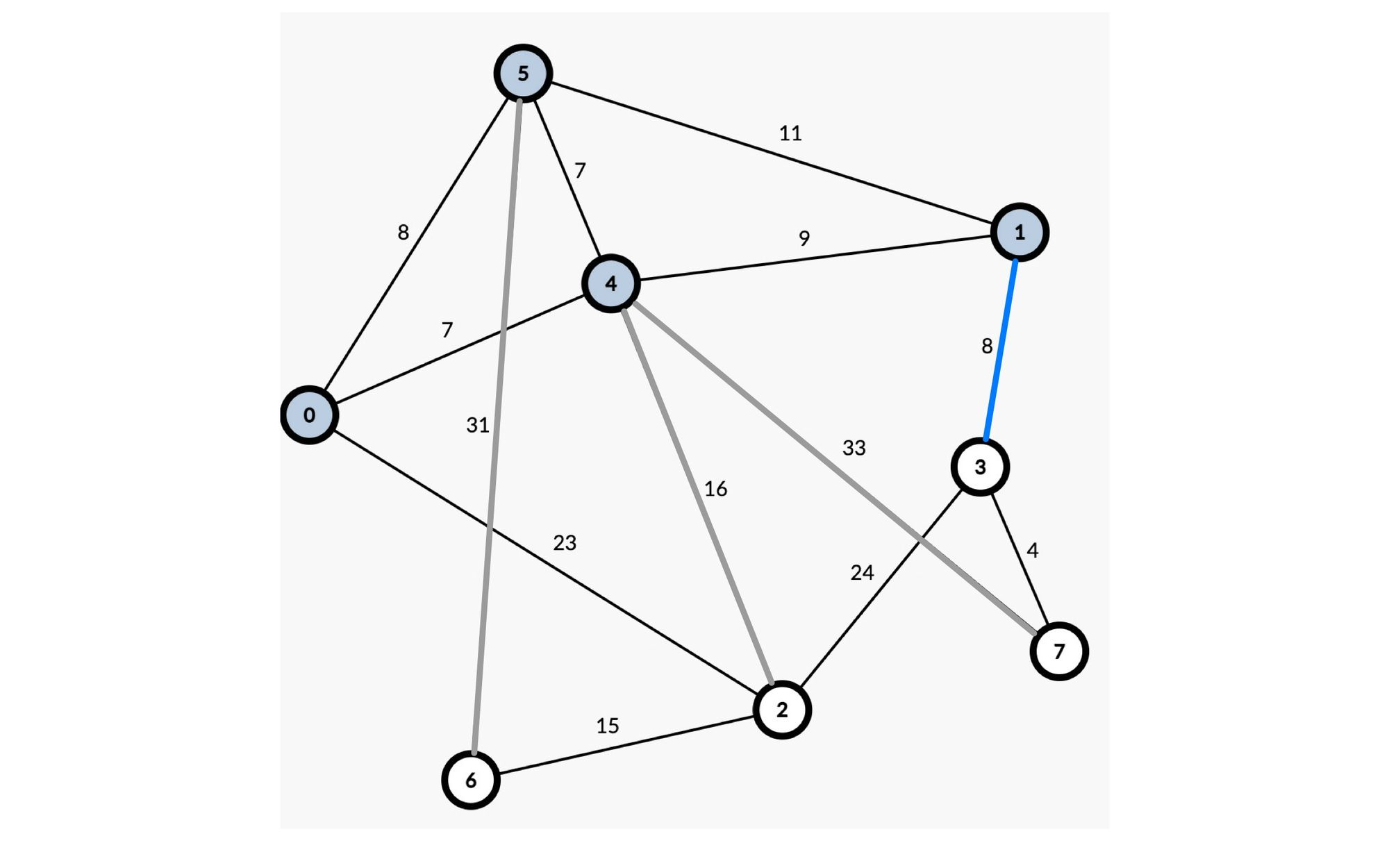
정점 $\{0, 4, 5, 1\}$에서 가장 가중치가 낮은 간선은 정점 3으로 가는 간선입니다. 그렇다면 이제 정점 3을 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신한 결과 한 노드로 가는 총 가중치가 바뀐 것을 알 수 있습니다(시작 정점 -> 정점 4 -> 정점 1 -> 정점 3 -> 정점 7)


정점 $\{0, 4, 5, 1, 3\}$에서 가장 가중치가 낮은 간선은 정점 7로 가는 간선입니다. 그렇다면 이제 정점 7을 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 이번에는 갱신할 노드가 보이지 않습니다.


정점 $\{0, 4, 5, 1, 3, 7\}$에서 가장 가중치가 낮은 간선은 정점 2로 가는 간선입니다. 그렇다면 이제 정점 2를 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신한 결과 한 노드로 가는 총 가중치가 바뀐 것을 알 수 있습니다(시작 정점 -> 정점 4 -> 정점 2 -> 정점 6)


정점 $\{0, 4, 5, 1, 3, 7, 2\}$에서 가장 가중치가 낮은 간선은 정점 6으로 가는 간선입니다. 그렇다면 이제 정점 6을 거쳐가는 경로를 모두 고려해서 최단 경로를 갱신하면 됩니다. 갱신이 되는 가중치는 없습니다.


이로써 모든 정점을 방문했습니다. 정점 0에서 시작해 각 정점을 방문하는 최소 가중치는 다음과 같습니다.
시작 정점 → 정점 1: 16
시작 정점 → 정점 2: 23
시작 정점 → 정점 3: 24
시작 정점 → 정점 4: 7
시작 정점 → 정점 5: 8
시작 정점 → 정점 6: 38
시작 정점 → 정점 7: 28
코드로 구현하면 아래와 같습니다.
typedef struct Graph {
int n;
int weight[MAX_VERTICES][MAX_VERTICES];
} Graph;
int distance[MAX_VERTICES]; /* 시작정점으로부터의 최단경로 거리 */
int found[MAX_VERTICES]; /* 방문한 정점 표시 */
int choose(int distance[], int n, int found[]) {
int min, minpos;
min = INT_MAX;
minpos = -1;
for(int i = 0; i < n; i++) {
if(distance[i] < min && !found[i]) {
min = distance[i];
minpos = i;
}
}
return minpos;
}
void print_status(Graph *g) {
static int step = 1;
printf("STEP %d: ", step++);
printf("distance: ");
for(int i = 0; i < g->n; i++) {
if(distance[i] == INF) {
printf(" * ");
} else {
printf("%2d ", distance[i]);
}
}
printf("\n");
printf(" found: ");
for(int i = 0; i < g->n; i++) {
printf("%2d ", found[i]);
}
printf("\n\n");
}
void shortest_path(Graph *g, int start) {
for(int i = 0; i < g->n; i++) { // 초기화
distance[i] = g->weight[start][i];
found[i] = FALSE;
}
found[start] = TRUE; // 시작 정점 방문 표시
distance[start] = 0;
for(int i = 0; i < g->n-1; i++) {
print_status(g);
u = choose(distance, g->n, found);
found[u] = TRUE;
for(int w = 0; w < g->n; w++;) {
if(!found[w]) {
if(distance[u] + g->weight[u][w] < distance[w]) {
distance[w] = distance[u] + g->weight[u][w];
}
}
}
}
}
'CSE > 자료구조 (data structure)' 카테고리의 다른 글
| [자료구조] 그래프 위상 정렬 알고리즘 (0) | 2022.11.08 |
|---|---|
| [자료구조] 플로이드(Floyd)의 최단 경로 알고리즘 (0) | 2022.11.07 |
| [자료구조] 프림(Prim)의 MST 알고리즘 (0) | 2022.11.05 |
| [자료구조] 크루스칼(Kruskal)의 MST 알고리즘 (0) | 2022.11.04 |
| [자료구조] 최소 신장 트리 (MST; Minimum Spanning Tree) (0) | 2022.11.03 |

컴퓨터 전공 관련, 프론트엔드 개발 지식들을 공유합니다. React, Javascript를 다룰 줄 알며 요즘에는 Typescript에도 관심이 생겨 공부하고 있습니다. 서로 소통하면서 프로젝트 하는 것을 즐기며 많은 대외활동으로 개발 능력과 소프트 스킬을 다듬어나가고 있습니다.
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[자료구조] 그래프 위상 정렬 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdpCK9P%2FbtrQezTd9yh%2FQkMlVB1ty1mk30SYPkMIk0%2Fimg.png)
![[자료구조] 플로이드(Floyd)의 최단 경로 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FlgaqG%2FbtrQgcvUD8C%2FKhK0cisGDr09fu10zKSKV0%2Fimg.png)
![[자료구조] 프림(Prim)의 MST 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbFG405%2FbtrQcM6jTT3%2FK6HAyIEKvCUDQQQ6ig82Lk%2Fimg.png)
![[자료구조] 크루스칼(Kruskal)의 MST 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FU0Xj4%2FbtrQeChAyHp%2FGGKij1x57h1a3ZQIqBb5T0%2Fimg.png)